Basic Antialiasing in RSL
Basic Antialiasing in RSL
July 1998
Abstract
Everybody has experienced it: sharp jaggies, pixellation artifacts, creepy-crawlies as the camera moves, horrible twinkling, or just plain weirdness when you pull back from your favorite procedural texture. It's aliasing, and it's a fact of life when writing shaders.
This talk is designed to make the problem seem less scary, to give you the conceptual tools to attack the problem on your own. It's not the be-all of antialiasing techniques, but it should get you started.
1 Introduction: Sources of Aliasing in Shading
What is aliasing, really? The heart of the problem lies in the domain of signal processing. Fundamentally, our conceptual model is that there is a continuous image function in front of the camera (or alternately, impinging on the film plane). But we want discrete pixels in our image, so we must somehow sample and reconstruct the image function. Conceptually, we want the pixel value to represent some kind of average measure of the image function in the area "behind" the entire pixel. But renderers aren't terribly good at computing that directly, so they tend to use point sampling to measure the scene at a finite number of places, then use that information to reconstruct an estimate of the image function. When the samples are spaced much closer than the distance between the "wiggles" of the image function, this reconstructed signal is an accurate representation of the real image function.
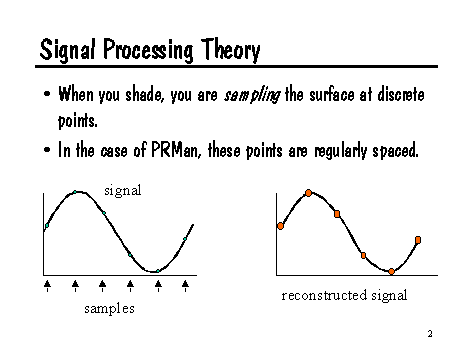
But when the samples aren't spaced closely enough, the trouble begins.
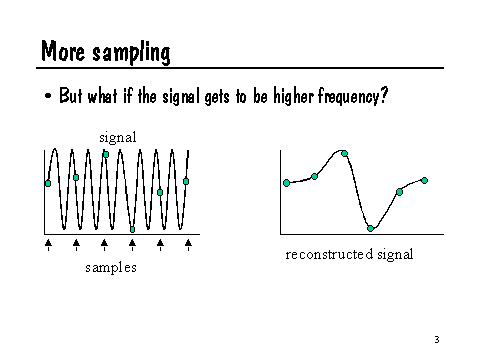
As illustrated by the previous slide, if the wiggles in the signal are spaced too closely (compared to the spacing of the samples), the wrong signal will be reconstructed. Specifically, highest frequency that can be adequately sampled is half the frequency of the samples themselves. This is known as the Nyquist limit. To put it another way, the samples must be at least twice the highest frequency present in the signal, or it will not adequately sample the signal.

The renderer executes the shader at discrete points on the surfaces, and this is a sampling problem. In fact, for PRMan in particular, the sampling of the shaders happens at regular intervals in parameter space. Regular samples are very prone to aliasing. In screen space, most renderers avoid aliasing by sampling geometry in a jittered fashion, rather than with regularly spaced samples. Jittering the samples replaces aliasing with noise, usually regarded as a less objectionable artifact (this is strictly a perceptual effect, a byproduct of our visual systems).

There are potentially two different sampling processes going on: the screen space samples and the shading samples in parameter space on the surface (for PRMan). Either one could cause aliasing if it is sampling a signal with frequencies above the Nyquist limit. For screen space samples, jittering replaces the aliasing with noise. This is a less objectionable artifact than aliasing, but it is still an artifact that can be avoided if we ensure that the image function itself has limited frequency content. But in PRMan the situation is worse, because by the time we are stochastically sampling in screen space, we have already taken regularly spaced samples in parametric space. In other words, the aliasing happens before the stochastic sampling can help. But even in a stochastic ray tracer, it would be better to be sampling an image function that didn't have frequencies beyond the Nyquist limit. We would like to prefilter the texture.
The key is realizing that the evils are all the result of point sampling the texture space function. Though we are making a single texture query, the reality is that this sample will be used to assign a color to an entire micropolygon or to color an entire pixel (or subpixel). Thus, our task is to estimate the integral of the texture function under the filter kernel that the sample represents. In other words, for a REYES-style micropolygon renderer, we want the average of the texture function underneath the entire micropolygon, rather than the exact value at one particular point on the micropolygon. For a ray tracer, we do not want to point sample the texture function, but rather we want the average value underneath the pixel that spawned the ray.
There are two trivial methods for estimating the average texture value under a region. First, you could use brute force to point sample several places underneath the filter kernel, and average those samples. This approach is poor because it merely replaces one point sample with many, which are still likely to alias, albeit at a higher frequency. Also, the cost of shading is multiplied by the number of samples that you take, yet the error decreases only as the square root of the number of samples.
The second trivial approach would be to generate the texture as an image map, a stored texture. RenderMan automatically antialiases texture lookups, so once the texture map is made (assuming that the generation of the texture map itself did not have aliasing artifacts), further use of the texture is guaranteed to antialias well with no need for you to worry about it in your shader. The problems with this approach mirror the downsides to texture mapping in general:
- there is a fixed highest resolution that is evident if you are too close to the surface;
- image texture maps have limited spatial extent and are prone to seams or obvious periodicity if they are tiled;
- high resolution stored textures can eat up a lot of disk space.
So assuming that we want to antialias a truly procedural texture, and don't feel that a valid option is to subsample the texture by brute force, we are left searching for more clever options. Sections 3 and 4 will explain two such strategies: analytic solutions to the integral, and frequency clamping methods. But first, Section 2 will review the Shading Language facilities that are needed for these approaches.

2 Shading Language Facilities for Filter Estimation
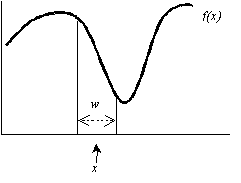
We've now recast the problem as estimating the average value of the texture function over an area represented by a sample (either a micropolygon or a pixel - it hardly matters which from here on, so I will sometimes interchange the terms). Pictorially, we have some function f that we are sampling at location x. But while we are supplied a single x value, we really want to average f over the range of values that x will take on underneath the entire pixel with width w:
The trick is, how big should w be in order to cover a pixel? Luckily, RSL provides us with methods for estimating the filter size w. In particular, there are three useful built-in functions:
- Du(x) returns the derivative of arbitrary expression x with respect to surface parameter u.
- Dv(x) returns the derivative of arbitrary expression x with respect to surface parameter v.
- Deriv(x,p) returns the derivative of expression x with respect to a unit change in expression p.
Okay, maybe only the first two are useful.
So we can take a derivative of an expression with respect to the u and/or v parameters of the surface, i.e. we know the rate of change, per unit of u or v, of x, at the spot being shaded. How does this help us estimate how much x changes from pixel to pixel? Two more built-in variables come into play:
- du is the change in surface parameter u between adjacent samples being shaded.
- dv is the change in surface parameter v between adjacent samples being shaded.
So if Du(x) is the amount that x changes per unit change of u, and du is the amount that u changes between adjacent shading samples, then clearly the amount that x changes between adjacent shading samples (moving in the direction of changing u) is given by:
Du(x)*du
And similarly, the amount that x changes between adjacent shading samples (moving in the direction of the v parameter) is:
Dv(x)*dv

Not only can we take these derivatives explicitly, but there are also some other built-in Shading Language functions that implicitly make use of derivatives:
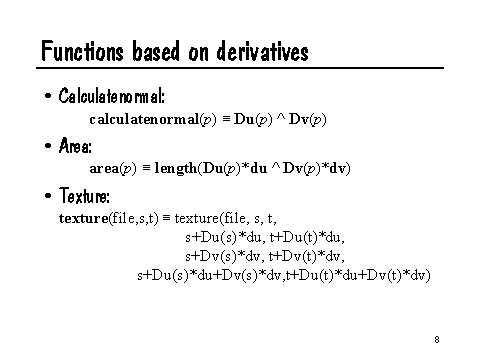
- calculatenormal(p) returns the cross product of the derivatives in each direction, i.e.
Du(p) ^ Dv(p)
- area(p) returns the (geometric) mean of the change of p between adjacent samples in each parametric direction,
length(Du(p)*du ^ Dv(p)*dv)
This is loosely interpreted as the area of the microfacet, if p = P.
- texture(filename,s,t) implicitly takes the derivatives of coordinates s and t to decide how large an area of texture to filter.
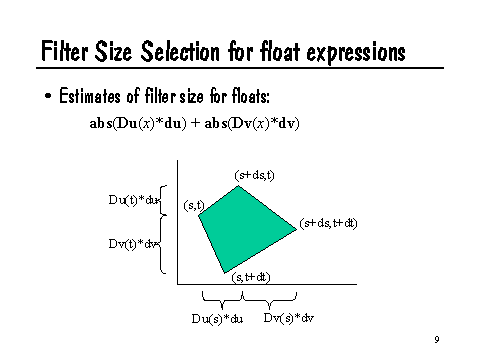
How can we use this information to estimate filter size? Recalling the expressions above for estimating how much x changes as we move one sample over in either u or v, a fair estimate of the amount that x will change as we move one sample over in any direction might be:
abs(Du(x)*du) + abs(Dv(x)*dv)
Informally, we are just summing the potential changes in each of the parametric directions. We take absolute values because we don't care if x is increasing or decreasing, we only are concerned with how much it changes between where we are and the neighboring sample. The geometric interpretation of this formula is shown in the following slide:
That formula works great if x is a float expression. But if x is a point, its derivative is a vector, and so the rest of the formula doesn't make much sense. But recall the definition of the built-in area() function:
area(p) = length(Du(p)*du ^ Dv(p)*dv)
The cross product of the two tangent vectors (Du(p)*du and Dv(p)*dv) is another vector that is mutually perpendicular to the other two, and has length equal to the "area" of the parallelogram outlined by the tangents. Hence the name of the function. Remember that the length of a cross product is the product of the lengths of the vectors. So the square root of area is the geometric mean of the lengths of the tangent vectors. Thus, sqrt(area(p)) is a decent estimate of the amount that point p changes between adjacent samples (expressed as a scalar).
With this knowledge, we can write macros that are useful for filter width estimates for either float or point functions:
#define MINFILTERSIZE 1.0e-6 #define filtersize(x) max (abs(Du(x)*du)+abs(Dv(x)*dv), MINFILTERSIZE) #define pfiltersize(p) max (sqrt(area(p)), MINFILTERSIZE)
The filtersize and pfiltersize macros can be used to estimate the change of its parameters from sample to sample, for float or point-like arguments, respectively. We impose a minimum filter size in order to avoid math exceptions if we divide by the filter size later. With these macros, we can move on to specific antialiasing techniques.

3 Analytic Antialiasing
Recall our earlier figure illustrating the function f, which we are trying to sample at x. We really want some metric of the average value of f in the region surrounding x with width w:
More technically, we want the convolution of function f and some filter kernel k having support of width w. Convolution is defined as:
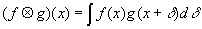
If we could use our knowledge of f to analytically (i.e. exactly, symbolically) derive the convolution F = f ⊗ k, then we could replace all references to f in our shader with F, and that function would be guaranteed not to alias.
3.1 Example: Antialiasing a Step Function
As an example, consider the built-in step(edge,val) function. This function returns 0 when val < edge, and 1 when val > edge. If we make such a binary decision when we are assigning colors to a micropolygon, the entire micropolygon will be "on" or "off." This will tend to produce "jaggies," a form of aliasing, as shown in the following image:
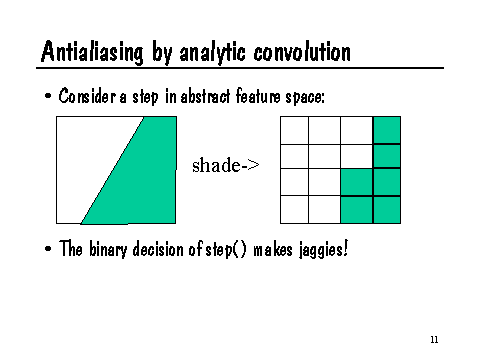
Can we construct a function, filterstep, that is the convolution of step with an appropriate filter kernel? Then we could use filterstep in place of step in our shaders and eliminate the resulting jaggies.
As usual for these problems, we must choose an appropriate filter kernel. For simplicity, let's just choose a box filter, because it is so easy to analyze. The adventurous reader may wish to derive a version of filterstep that uses, say, a Catmull-Rom filter.

An intuitive way of looking at this problem is: for a box filter of width w centered at value x, what is the convolution of the filter with step(e,x)?
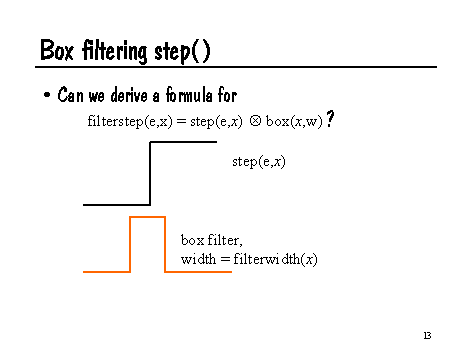
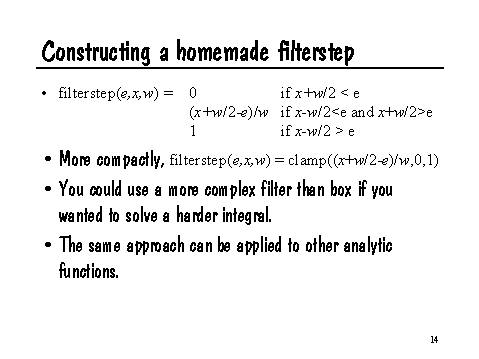
This problem is easy to analyze. If (x+w/2) < e, then the result of filterstep is 0, because the box filter only overlaps the part of step that is zero. Similarly, if (x-w/2) > e, then filterstep should return 1, since the filter only overlaps the portion of step that is 1. If the filter overlaps the transition e, then filterstep should return the fraction of the filter that is greater than e, in other words, (x+w/2-e)/w. As a further optimization, note that we can express this in RSL very compactly
float filterstep (float edge, float x, float w)
{
return clamp ((x+w/2-e)/w, 0, 1);
}
(Can you convince yourself that this is correct?) Of course, the w you supply to this function is properly the filter width returned by the macros we discussed earlier.
Note that we made a compromise for simplicity: we generated the antialiased version of step by convolving with a box filter. It would be better to use a Catmull-Rom, or other higher quality filter, and for a function as simple as step, that wouldn't be too hard. But for more difficult functions it may be very tricky to come up with an analytic solution to the integral when convolved with a nontrivial kernel. So we can often get away with simplifying the integration by assuming a simple kernel like a box filter.
As an aside, there's now a built-in SL function, filterstep, which does exactly what we've described. It's been in PRMan since release 3.5. The syntax differs slightly from what we have described above. In particular, you don't need to supply the filter width - filterstep will automatically compute it, much as texture does with its arguments. Also, the built-in filterstep takes optional parameters allowing you to specify exactly which filter to use and how to modulate its width. Please see the filterstep documentation for details.

3.2 More Complex Examples
As another example, consider the function:
float pulse (float edge0, edge1, x)
{
return step(edge0,x) - step(edge1,x);
}
This is a useful function which returns 1 when edge0 <= x <= edge1, and 0 otherwise. Like step, it aliases horribly at any sampling rate, since it has infinite frequency content. And here is its antialiased version:
float filteredpulse (float edge0, edge1, x, fwidth)
{
float x0 = x - fwidth/2;
float x1 = x0 + fwidth;
return max (0, (min(x1,edge1)-max(x0,edge0)) / fwidth);
}
It is left as an exercise for the reader to verify this derivation.
One last, less trivial, example of analytic antialiasing involves antialiasing a pulse train. Such a function is shown in the following figure:
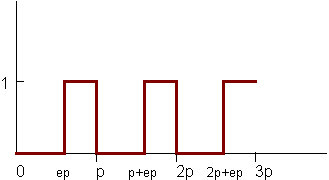
Here is this function expressed in RSL:
/* A pulse train: a signal that repeats with a given period, and is
* 0 when 0 <= mod(x/period,1) > edge, and 1 when mod(x/period,1) > edge. */
float pulsetrain (float period, edge, x)
{
return pulse (edge, 1, mod(x/period, 1));
}
Attacking this function is more difficult. Again, we will assume a box filter, which means that filteredpulsetrain(period,edge,x,w) is:
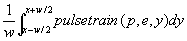
This integral is actually not hard to solve. First, let's divide x and w by period, reducing to a simpler case where the period is 1. Here is a graph of the accumulated value of the function between 0 and x:
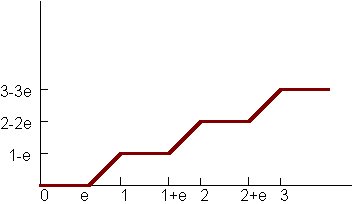
This function is given by F(x) = (1-e)floor(x) + max(0, x-floor(x)-e). Can you convince yourself that this is true? If the accumulated sum of f(x)- in other words, the indefinite integral - is F, then the definite integral
Therefore the following code implements a filtered pulse train:
/* Filtered pulse train: it's not as simple as just returning the mod
* of filteredpulse -- you have to take into account that the filter may
* cover multiple pulses in the train.
* Strategy: consider the function INTFPT, which is the integral of the
* train from 0 to x. Just subtract!
*/
float filteredpulsetrain (float period, edge, x, width)
{
/* First, normalize so period == 1 and our domain of interest is > 0 */
float w = width/period;
float x0 = x/period - w/2;
float x1 = x0+w;
/* Now we want to integrate the normalized pulsetrain over [x0,x1] */
#define INTFPT(x) ((1-edge)*floor(x) + max(0,x-floor(x)-edge))
return (INTFPT(x1) - INTFPT(x0)) / (x1-x0);
#undef INTFPT
}
This code works well even when the filter size is larger than the pulse period. Here is an example of a pattern based on pulsetrain (left), versus the filtered version using the function above (right):
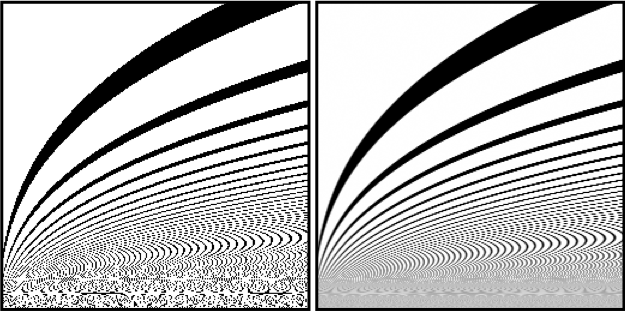
Note that there is still some bad ringing. This is a result of our use of a box filter - it's not very good at clamping frequencies. A better filter would have less ringing, but would have a more difficult integral to solve. Nonetheless, the most insidious aliasing is gone.
4 Antialiasing by Frequency Clamping
You will find that your favorite Shading Language functions fall into three categories:
- functions for which you can trivially derive the convolution with a filter kernel, probably a box filter;
- functions that are really hard to integrate analytically - lots of work, some integral tables, and maybe a session with Mathematica will help;
- functions that don't have an analytic solution, or whose solution is just too hard to derive.
Many useful functions fall into the third category. Don't worry, just try another strategy. In general, the next best thing to an analytic solution is frequency clamping. The basis of this approach is to decompose your function into composite functions with known frequency content, and then to only use the frequencies which are low enough to be below the Nyquist limit for the known filter size.
The general strategy is as follows. Suppose you have a function g(x) that you wish to antialias, and your computed filter width is w. Suppose further that you know the following two facts about your function g:
- Function g has features (the "wiggles" of the function) no smaller than width f.
- The average value of g, over large ranges of values, is a.
We know that when w << f/2, we are sampling areas of g much smaller than its smallest wiggles, so we will not alias. If w >> f/2, we are trying to sample at too high a frequency and we will alias. But we know the average value of g, so why not substitute this average value when the filter is too wide compared to the feature size? More formally,
#define fadeout(g,g_avg,featuresize,fwidth) \
mix (g, g_avg, smoothstep(.2,.6,fwidth/featuresize))
This simple macro does just what we described. When the filter width is small compared to the feature size, it simply returns g. When the filter width is too large to adequately sample the function with that feature size, it returns the known average value of g. And in between, it fades smoothly between these values.

As an example, let's look at the noise function. We use it in shaders all the time. It will alias if there are fewer than two samples per cycle. We know that it has a limited frequency content - the frequency is approximately 1. We also know that its average value is 0.5.
But noise is often less useful than its cousin, snoise (for Signed noise). We usually define snoise as follows:
#define snoise(x) (2*noise(x)-1)
Regular noise has a range of (0,1), but snoise ranges on (-1,1) with an average value of 0. Consider the following macro:
#define filteredsnoise(x,w) fadeout(snoise(x), 0, 1, w)
This macro takes a domain value x, and a filter width w, and returns an (approximately) low pass filtered version of snoise. Okay, we all know it's not really low pass filtered noise - it fades uniformly to the average value of noise, just as the frequency gets high enough that it would tend to alias.

We can extend this to make a filtered version of fractional Brownian motion - that's the technical term for summing successively higher octaves of noise at successively lower amplitudes.
float filtered_fBm (point p, float octaves, float lacunarity, float gain)
{
uniform float i;
uniform float amp=1, freq=1;
varying float fw = pfilterwidth(p);
for (i = 0; i < octaves; i += 1) {
sum += amp * filteredsnoise (p*freq, fw);
amp *= gain; freq *= lacunarity; fw *= lacunarity;
}
return sum;
}
As noted earlier, this isn't a truly correct filtered noise. Rather than correctly low pass filtering the noise function, we are simply omitting (or fading out) the octaves which are beyond the Nyquist limit. This can lead to artifacts, particularly when the filter width is so large that even the lowest frequencies in the fBm will fade to their average value of 0 - in other words, the entire function will fade to a flat color with no detail.
5 Conclusions and Caveats
This chapter has outlined two methods for antialiasing your procedural shaders. Unfortunately, it's still a hard task. And these methods, even when they work fine, are not without their share of problems:
While analytic integration yields exact antialiased results, only a few (generally simple) functions have analytic solutions that exist and are easy to derive.
Frequency clamping and global fading are applicable to more complex functions, but they are not really the same as low pass filtering, and artifacts may result. (But those clamping artifacts are probably less objectionable than horrible aliasing.)
Both methods can suffer from the fallacy of composition: for functions f and g and filtering kernel k, if you know the low-pass-filtered versions F = f ⨂ k and G = g ⨂ k,
F(G(x)) ≠ (f(g) ⨂k)(x) in general
In other words, convolution does not necessarily hold across the composition of functions. What this means is that you cannot blindly replace all your step calls with filterstep, and your noise calls with filternoise and expect thresholded noise to properly antialias.
Previous versions of PRMan had du and dv estimates that were constant across each grid. That meant that any filter size estimates that depended on derivatives (as all the ones discussed in this paper do) potentially had discontinuities at grid boundaries. This was a particularly evil problem when dealing with displacements, as discontinuities of displacement amounts across grid boundaries can result in cracking
We've been restricting our discussion to color, and displacement is even trickier. Consider a surface that is displaced with a noise field. If we use the filtered noise to antialias the bumps, what happens as we approach the Nyquist limit and the bumps fade down? A flat surface catches and reflects light much differently than a rough surface, so you may notice a light or color shift that you didn't want. This is a common problem when antialiasing bumps or displacements, and I have yet to see a satisfactory solution that works in the general case.

These are only the basics, but they're the bread-and-butter of antialiasing, even for complex shaders. Watch out for high frequency content, conditionals, etc., in your shaders. Always try to calculate what's happening under a filter area, rather than at a single point. Don't be afraid to cheat - after all, this is computer graphics. And above all, have fun writing shaders!
