The Ins And Outs of PRMan
The Ins And Outs of PRMan
October 2012
Introduction
This application note elaborates on what it means to be "outside" in RenderMan, expands upon issues related to double-shaded geometry, and discusses several common pitfalls associated with determining the outside of a surface in the RenderMan Shading Language.
Defining the Outside
Key to understanding the RenderMan definition of the "outside" of a surface is understanding how normals are oriented, which itself requires understanding how orientation works in RenderMan.
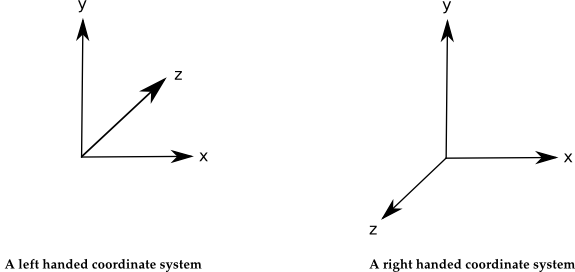
The RenderMan Specification discusses orientation in two separate but conjoined contexts. First, there is the orientation of a coordinate system, which is defined to be its handedness: whether the left-hand or right-hand rule is used to determine the relative directions of the x-, y-, and z-axes. Therefore, we can talk about the orientation of the coordinate system as being either left-handed or right-handed. In RenderMan, the default orientation of the camera coordinate system is left-handed. Transformations applied to a coordinate system may flip the orientation of the coordinate system (i.e: cause a left-handed orientation to become right-handed); we can infer whether a transformation will have this effect by taking the determinant of the matrix defining the transformation. If the determinant is negative, the orientation will flip.
The second context in which orientation is important is the inherent orientation of a geometric primitive, which is used to decide how the surface normals are oriented relative to the primitive in its own (object) coordinate system. For geometry types that explicitly require RI_P in the object definition, a left-handed orientation of the geometry means that a left-handed rule is applied to the vertices to determine the orientation of the normal; likewise, a right-handed orientation means a right-handed rule is applied to the vertices. Thus, we can also talk about the orientation of geometry as being either left-handed or right-handed.
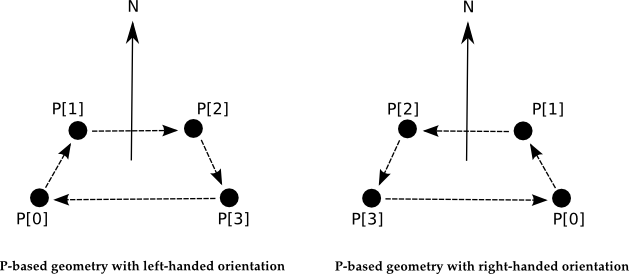
The orientation of geometric primitives can be defined relative to the orientation of the current coordinate system by specifying "outside" or "inside"; it can be explicitly overridden by specifying "lh" or "rh"; or it can be toggled from its current state by using RiReverseOrientation. It is important at this stage to understand that defining the orientation of a primitive to be opposite that of the object coordinate system causes the primitive to be turned inside-out, which means its normal will be computed so that it points in the opposite direction than usual. Note that PRMan sometimes uses the word "backfacing" to mean "inside-out".
At this juncture, we should note a special case for geometry types that do not require RI_P in the object definition - most notably, quadrics - for which winding order is not applicable. For these primitives RenderMan adopts the convention that if the orientation of the geometric primitive matches the orientation of the current coordinate system, the normal orientation is the "natural" orientation (which generally faces "outward", i.e. in the case of a sphere, away from the center of the sphere). Otherwise, if the orientation does not match, we also turn these primitives inside-out: the normal orientation is the opposite orientation, i.e. in the case of a sphere, they are oriented towards the center.
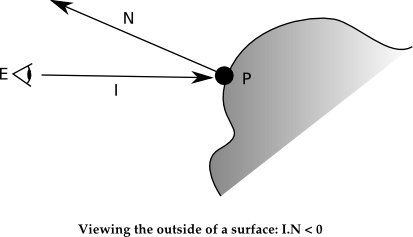
With this understanding of orientation, we can now start understanding what it means to be on the outside of a surface and how that changes with the orientation. First, we adopt the definition (again, straight out of the RenderMan specification) that the "outside" surface is the side from which the normals point outward. This definition may be somewhat imprecise to the mathematical mind. We can try to close the gap by stating that given a vantage point E, a shading point P, and a normal N associated with that shading point P, the shading point P represents the outside of the surface as viewed from the vantage point E if the dot product of the vector I = P - E and N has a negative sign. Not by coincidence, the choice of these letters maps exactly to shading language definitions.
Outside Versus Inside
Simply being on the outside or the inside of a surface has several ramifications in RenderMan. We will skip the obvious fact that the normals are different on the outside or inside of a surface, since the definition of being outside is tied up with the normals. (At the same time, we should not underplay the importance of the correct orientation of normals, as they are critically important to lighting and ray tracing.)
The most obvious issue is backface culling. If Sides 1 is enabled, subsequent geometry is deemed one-sided. This means that any geometry that is deemed to be "outside" from the vantage point of the camera is considered to be visible; all other ("inside") geometry is invisible and culled. In cases where modeling software produces a geometry definition with an orientation that does not match the orientation of the camera, this may lead to an undesired backface culling result. This is typically fixed by inserting a ReverseOrientation directive to reverse the orientation of the geometry definition to match the camera.
Important
Backface-culling was not implemented correctly when using the ray trace hider in versions of PRMan prior to 17.0.
Backface-culling does not only apply to geometry seen from the vantage point of the camera. Most ray tracing shadeops accept the optional hitsides parameter. When this parameter is set to front, and the geometry that is being intersected is one-sided, the ray will not hit the geometry if it is considered to be "inside" from the vantage point of the ray origin (E).
Another, somewhat less obvious issue pertains to radiosity caching in the context of ray tracing. Without ray tracing or reflection mapping, geometry can be viewed only from the camera, so we typically do not need to shade both the outside and inside of a surface as only the outside is visible. Once ray tracing is added to a scene, rays may be reflected in ways that lead to both the outside and the inside of a surface being visible. The irradiance on each side of the surface may differ considerably and must be cached separately. This aspect of radiosity caching is handled transparently by the renderer.
Double Shading - What and Why?
PRMan has a special attribute that enables double-sided shading ("double shading" for short). Double shading is best understood as explicitly turning a piece of geometry into two separate, backface-culled, one-sided surfaces, regardless of the original Sides setting. One of these surfaces will end up with the same orientation as the original geometry and the other surface explicitly reverses the orientation. This means that one surface is explicitly outside-out and the other is explicitly inside-out; it is important to realize that the surface that ended up inside-out may or may not be the same as the original one-sided geometry.
As a result of double shading, we end up with two surfaces whose surface normals are exactly opposite each other. Thus, ignoring displacement for the moment, at any shared point on these two surfaces and from any given vantage point relative to that shared point, one surface can always be considered "inside", while the other surface will be considered "outside". If we then take backface culling into account, from any vantage point we will only be able to see one of these two surfaces (the "outside" one), because the inside surface will be backface-culled. Therefore, another side effect of double shading is: given any undisplaced surface point P belonging to the double-shaded geometry and any vantage point E that has an unoccluded view of that surface point, the normal of the surface always faces that vantage point.
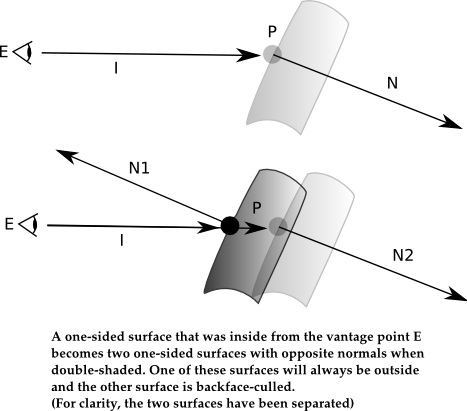
Double-shaded geometry (geometry with Attribute "sides" "int doubleshaded" [1]) differs from two-sided geometry (geometry with Sides 2, "doubleshaded" [0]) in several key aspects.
As described above, the normal on a double-shaded surface always faces any vantage point. This is certainly not always true for two-sided geometry. This can be a desired and useful side effect; it allows for a single piece of geometry modeled as a sheet to be easily displaced in both directions (along the two disparate sets of N) to create a new geometry that has shader-generated thickness.
Anyone who writes a displacement shader that does this should be aware that it is the shader writer's responsibility to ensure the resulting displaced object is a closed surface. Otherwise, what may occur is that the displacement leads to a situation where the inside of the displaced object is no longer occluded by any other part of the object that is outside. Since all parts of the object are considered backface-cullable, this will lead to holes. Ensuring the object remains closed through displacement can be trivially accomplished by clamping the displacement to zero at the parametric edges of the object. An example of such a trivial shader follows; this shader is meant to be applied to a cylinder, which is why there is no parametric clamp at the s=0 and s=1 edges of the object.
displacement sins(float height = 0.5; float frequency = 5) {
float s2c_scale = length(ntransform("shader",N))/length(N);
float sbmp = 0.5 * (sin(s * 2 * 3.1415926535 * frequency) + 1);
float tbmp = 1;
if (t < 0.1) {
tbmp = t * 10;
} else if (t > 0.9) {
tbmp = (1 - t) * 10;
}
P += (sbmp * tbmp) * height * normalize (N) * s2c_scale;
N = calculatenormal(P);
}
The effect of rendering double-shaded geometry is defined to be exactly equivalent to running the shader twice, once for each copy of the one-sided surface. In many cases, the renderer may perform an optimization and will not actually run the shader twice, so long as the rendered result is the same. For example, this often will occur if no displacement shader is bound to the geometry, and the inside portion of the geometry is never seen from the camera. However, it is also equally true that the renderer often cannot perform this optimization and is required to run the shader twice.
For two-sided geometry, the opposite is true: the renderer generally never needs to run the shader twice. (An exception to this rule has already been mentioned: two-sided geometry may be shaded twice for the radiosity cache.)
The take away from this is: double-shaded geometry is never cheaper than two-sided geometry, and is often more expensive to shade. Therefore, if an effect can be accomplished by leaving the geometry two-sided it is more efficient to do so.
One important scenario in which the extra cost of double shading (versus two-sided geometry) may be desirable, even when displacement is not involved, is when shading a piece of geometry with different colors on each side. Suppose we are rendering a single sheet, red on one side and green on the other, which is twisted once, relative to the camera, so that part of the red and part of the green sides end up visible. If we designated this geometry as being two-sided and not double-shaded, since this geometry is conceptually shaded only once we may end up with some micropolygons where half of the vertices are red and half of the vertices are green. If these micropolygons are large (ShadingRate is coarse), the rendered image at those micropolygons may end up being incorrect. ShadingInterpolation may minimize but not entirely eliminate these errors.
On the other hand, we can eliminate these errors by designating the geometry as being double-shaded and not two-sided - so long as we ensure that the shader consistently shades one side of the surface entirely red and one side entirely green. This ends up working because when using the standard REYES hider, backface culling occurs at a higher frequency than shading, and guarantees that no part of the micropolygon that might be twisted away from the camera is visible. Conceptually: where in the two-sided case we could end up with one micropolygon with half its vertices red and half its vertices green, in the double-shaded case we would instead have two micropolygons, one entirely red and one entirely green, and backface culling guarantees that only the correct portion of each micropolygon is visible. This situation is illustrated below. Note that a similar situation may occur not only with bowtie micropolygons; it may occur at terminator regions, where a micropolygon has normals both facing towards and away from the camera.
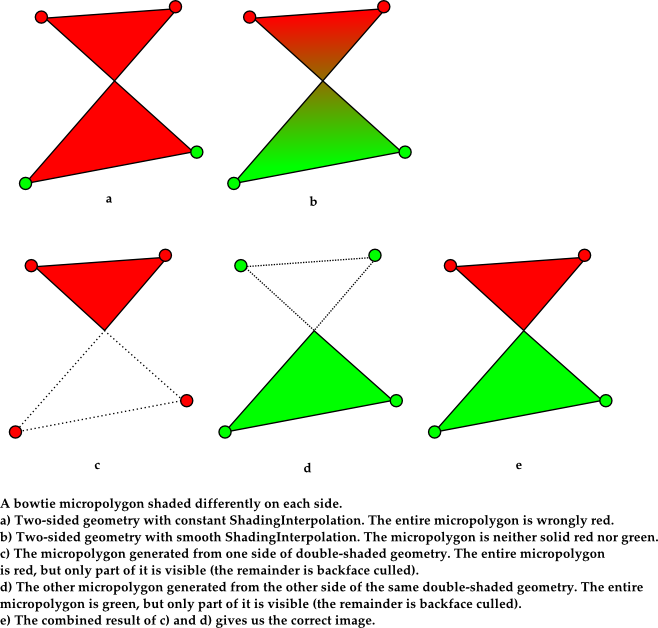
Important
Double shading was not implemented correctly in ray tracing for versions of PRMan prior to 17.0. In particular, displacement during double shading was ignored; double-shaded geometry was incorrectly radiosity cached; and the treatment of normals was often incorrect, most often in right handed coordinate systems.
Determining the Outside in Shading
Given all this, suppose we decide to write a shader that shades the two sides of a surface with different colors. Furthermore, suppose we decide that the outside should be colored green, and the inside should be colored red. And finally, given the caveat about two-sided geometry being cheaper than double-shaded geometry, for now let's assume we are dealing strictly with two-sided geometry.
Given the previous mathematical definition of outsideness, it is tempting to simply decide that a dot product between I and N is all we need to write this shader:
surface redgreen() {
if ((N . I) > 0) {
Ci = color(1, 0, 0);
} else {
Ci = color(0, 1, 0);
}
}
Unfortunately, this shader works in some, but not all circumstances. Before explaining these circumstances, let's digress slightly and discuss how PRMan computes normals in the first place. Given a parametric surface with a position P parameterized by u and v, PRMan computes the parametric derivatives dPdu and dPdv. The surface normal is computed by taking the cross product of these two derivatives: N = dPdu x dPdv - but only if the current geometric orientation matches the orientation of the current coordinate system. Otherwise, the normal is flipped, which is akin to taking the cross product the other way: N = dPdv x dPdu. If we relied solely on this N computed via the cross product, the N.I test would (mostly) work.
However, there is an important circumstance in which N is not the result of the cross product of dPdu and dPdv. This involves user normals supplied explicitly with the geometry (e.g. smoothed user normals attached to a RiPointsPolygon invocation). When user normals are supplied, they are interpolated based on the parametric definition but they are never automatically flipped by the renderer if the orientation of the surface does not match the orientation of the current coordinate system, i.e. if the surface is "inside-out". As a result of this, when using the above redgreen shader, the answer of "outside" vs "inside" does NOT reverse when the orientation of the geometry is flipped by, e.g., a ReverseOrientation call if user normals are attached. (There is an exception to this rule: if the surface is double-shaded, user normals are flipped for one of the sides.)
A savvy shader writer may attempt to circumvent this situation by encoding a special case to reverse the normal if the surface is "inside-out" by checking the geometry:backfacing attribute and reversing the normal. Such a shader could only be used in situations where user normals are supplied, since the normal would already be reversed when the user normal is not supplied (and automatically detecting this situation is generally not possible).
surface redgreen() {
float side, NdotI;
attribute("geometry:backfacing", side);
if (side == 1) {
NdotI = -N.I;
} else {
NdotI = N.I;
}
if (NdotI > 0) {
Ci = color(1, 0, 0);
} else {
Ci = color(0, 1, 0);
}
}
Unfortunately, confusing the issue further, this shader will no longer work in certain situations if displacement occurs! To understand this issue, we have to examine the calculatenormal() shadeop, which is called either explicitly by the shader writer, or may be called implicitly if P is altered; either way, N generally ends up altered. The calculatenormal shadeop computes a new normal based on computing forward differences of P and automatically reverses the normal if the surface is inside-out. It does this even if the original normal N came explicitly from user supplied normals. Because of this, we are left with the curious situation whereby geometry with user-supplied normals may have its normals explicitly reversed after displacement occurs, if that geometry was inside-out to begin with. As a result, the N dot I test must now take into account whether or not displacement has occurred and adjust its backfacing check.
Even if we can correct for all these cases (or simply avoid them), double shading throws us yet another curveball. We could simply ignore double shading and continue to use the dot product - but as noted above, one reason to turn on double shading for this type of shading work is to avoid artifacts. And to avoid these artifacts, we specifically want to avoid the dot product, or more generally avoid any determination of outsideness that is varying (and is therefore bounded by the shading frequency). Instead, we rely on a uniform answer to consistently shade each one-sided surface red or green, and let visibility determination cull away the portion of the shaded result which is considered inside at the higher visibility frequency.
It should now be obvious that creating a simple redgreen shader that works in all circumstances is difficult at best.
The Outside Solution
Given these difficulties (and many others), PRMan 17 solves the problem of tracking the outside of a surface by doing it for you. A new query to the attribute() shadeop has been added: geometry:outside. The value returned in the result is 1 if the current point is the outside of the surface, 0 otherwise. It is handles all of the aforementioned problems related to user normals, displacement, etc., and is also guaranteed to be correct through shading for ray-traced caching purposes, ray-traced tessellation, etc. Moreover, it gives the correct uniform-like answer for double shaded geometry, which can be relied upon to avoid artifacts for disparate sided shading. With this attribute, we can now write the redgreen shader as simply as this:
surface redgreen() {
varying float outside;
attribute("geometry:outside", outside);
if (outside == 1) {
Ci = color(0, 1, 0);
} else {
Ci = color(1, 0, 0);
}
}
Unlike other queries to the attribute() shadeop, geometry:outside explicitly requires that the result variable is varying. Furthermore, making this query has no deleterious effect on whether or not grids can be combined for shading. However, the fact that "geometry:outside" is varying precludes queries of it using the Rx interface, even from RSL plugins.
