Blobby Implicit Surfaces
PhotoRealistic RenderMan
Application Note #31
Blobby Implicit Surfaces
September, 1999Introduction
Note
Please set your monitor gamma to 2.3 or thereabouts. Otherwise the pictures will look dark and ugly. If they're ugly but not dark, your gamma is ok.
Photorealistic RenderMan now supports a new surface type,
RiBlobby, to render blobby implicit surfaces in the style of
Blinn's blobby molecules, Nishimura et al's Metaballs and
Wyvill et al's soft objects.
Blobby models are built from simple primitive shapes
(ellipsoids and sausage-like
cylinders with rounded ends in the current implementation) blending
together into rounded, tubby, globular masses.
They are best used in situations where users want to model amorphous
shapes and are willing to trade away fine control over details of shape
for ease of modeling gross features.
Jim Blinn's models of complex
molecular structures and the splatting raindrops in A Bug's Life are
good applications of Blobby models.
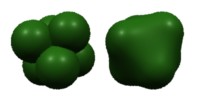The most important feature of blobby implicit models is automatic
blending. Blobby shapes placed close to one another can be blended
together (or not, as the modeler wishes) with no need for modelers to
construct explicit round and fillet patches joining them. The two objects
in the picture to the left contain identical clusters of spheres: unblended on the left,
blended on the right.
Blending is not an all-or-nothing proposition.
For example, we can model a blobby hand to blend the fingers into the
palm, but completely prevent fingers from blending into one another.
The picture below shows an extremely ugly space-alien hand, first with no
blending, then with all ellipsoids blended together, then with selective
blending to prevent webs from growing between the fingers.
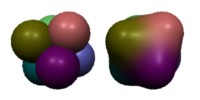RiBlobby also allows modelers to attach values of any Shading Language
type to individual blobs. These will be blended appropriately and passed
to surface and displacement shaders in the usual way. The image on the left
shows the same two sphere clusters we saw before, this time with different
values of Cs given for each sphere. When
the spheres are not blended, there is no color bleed from one to the other;
when they are blended, the colors blend likewise.
RiBlobby also has a segment blob primitive. Segment
blobs are a simple sort of convolution surface
(see J. Bloomenthal and K. Shoemake,
``Convolution Surfaces,''
Computer Graphics, v25, n4, 1991,
pp 251-256),
so they add without seams or bulges to make general
tubular surfaces with piecewise
linear skeletons. The surface in the picture on the left is the sum of 480 segment
blobs in a toroidal spiral.
Solid-texture coordinate systems may likewise be attached to individual
blobs and blended to provide global texture coordinates, as in this striped
blob-chain. Each of its twenty constituent spheres has attached a
transformation that carries points from the object coordinate
system to a reference space. When the chain is laid out straight, these
two coordinate systems are identical. When the chain is coiled up, each
transformation carries its sphere back to its position in the reference
space. Coordinate blending between adjacent spheres stretches the
mapping just enough to keep the solid texture attached to the surface
as it bends.
Blobby implicit surfaces often get used
to model drops of liquid that need to interact with other surfaces in the
scene. As an aid for this situation, RiBlobby also allows ground
planes represented as prman z-files to act as repelling surfaces.
This feature allows the user substantial control over the nature
of the repulsion. In this image the roundedness of the displaced blob
surface, its bulginess near the ground and even how far it hovers over
the repeller are all controllable over a wide range.
Blobby Principles
Most of prman's surface types have explicit control meshes. That is, the geometry is specified by a network of points in object space that are on or near the surface. RiBlobby surfaces are defined implicitly, by a continuous field functionF(x, y, z) that is equal to some threshold value T at every point on the surface. A simple example of an implicit-function surface is the well-known equation of the sphere with center at the origin and radius D, which is x2+y2+z2=D2The only serious problem with using this equation to represent a sphere is that since F gets large as we move away from the origin, it's hard to combine this with other spheres in any meaningful way. RiBlobby gets around this by using a slightly different field function that is 1 at the origin and goes to zero at some finite distance. If we write R2=x2+y2+z2, the function is
-
F(R)=1-3R2+3R4-R6, whenever R<=1
and
F(R)=0 when R>1
Of course, we can combine primitive blobs in other ways. For example,
if we take a small blob and subtract its field from a larger one, we
can put a dent in it. If we transform the
subtracted blob to be long and thin enough,
we can even poke a hole through the larger one.
On the other hand, if we take the max of the two primitive fields
instead of subtracting, the result is an (unblended) union of the primitive
surfaces. The selectively blended hand, above was made
by a more complicated combination. For each of the four fingers, the blobs
describing it were added together, along with two or three adjacent blobs
at the edge of the palm.
A separate added-together group was made of all the palm blobs. The whole
field function was just the max of these five overlapping blending
groups.
API
Now that we've seen most of the underlying details, we can get down to brass tacks. In the RenderMan C binding, blobby implicits are specified byvoid RiBlobby( RtInt nleaf, RtInt ncode, RtInt code[], RtInt nflt, RtFloat flt[], RtInt nstr, RtString str[], ...);In a RIB stream, the syntax is
Blobby nleaf [ code ] [ floats ] [ strings ] parameterlist
The code array is a sequence of machine language-like instructions describing the object's primitive blob fields and the operations that combine them. Floating point parameters of the primitive fields are stored in the floats array. File names of the z-files of repellers are in the strings array. The integer nleaf is the number of primitive blobs in object, also the number of items in each varying or vertex parameter.
Each instruction has a numeric opcode followed by a number of operands. Instructions specifying primitive fields start at 1000. They are:
| Opcode | Operands | Operation |
|---|---|---|
| 1000 | float | constant |
| 1001 | float | ellipsoid |
| 1002 | float | segment blob |
| 1003 | string, float | repelling ground plane |
For all four of these operators, the operands are indices into the appropriate arrays.
- For opcode 1000 (constant) the operand indexes a single floating-point number in the floats array. The index of the first item in the array is zero.
- For opcode 1001 (ellipsoid) the operand indexes the first of 16 floats describing a 4x4 matrix that transforms the unit sphere into the ellipsoidal bump in object space.
- The operand of opcode 1002 (segment blob) indexes 23 floats that give the endpoints and radius of the segment and a 4x4 matrix that transforms the segment into object space. The segment blob's field is just the convolution of a `segment impulse' with the same spherical bump used for ellipsoid blobs.
- Opcode 1003 (repelling ground plane) takes two indices. The
first gives the index of the name of a z-file in the strings array.
The second indexes the first of 4 float parameters of the repeller's
repulsion contour.
The value of the field generated by a repeller is a function of the vertical
distance from the evaluation point to the z-file, in the view direction in
which the z-file was generated. The four float parameters control the shape of
the repelling field. Let's call the four parameters A, B, C and D. A controls
the overall height of the repeller. The field value is zero whenever the
height above the ground plane is larger than A. B controls the sharpness
of the repeller. The field looks a lot like -B/z (except that it fades to zero
at z==A, and remains at a large negative value when z<0),
so smaller values of B place the knee in the curve closer to z==0.
Added to this negative-going barrier field is a bump that
has its peak at z==C, and whose maximum value is D. The bump component
is exactly zero outside the range 0<=z<=2*C. If you're interested
in all the gory details, here is a short C program that computes the
repulsion field:
/* * When 0<=r<=2, bump(r) is the polynomial of lowest degree with * bump(0)=0 * bump'(0)=0 * bump"(0)=0 * bump(1)=1 * bump(2)=0 * bump'(2)=0 * bump"(2)=0 */ float bump(float r){ if(r<=0. || r>=2.) return 0.; return (((6.-r)*r-12.)*r+8.)*r*r*r; } /* * When 0<=r<=1, ease(r) is the polynomial of lowest degree with * ease(0)=0 * ease'(0)=0 * ease(1)=1 * ease'(1)=0 */ float ease(float r){ if(r<=0.) return 0.; if(r>=1.) return 1.; return r*r*(3.-2.*r); } #define ZCLAMP 1e-6 float repulsion(float z, float A, float B, float C, float D){ if(z>=A) return 0.; if(z<=ZCLAMP) z=ZCLAMP; return (D*bump(z/C)-B/z)*(1.-ease(z/A)); }
There are several more opcodes that compute composite fields by combining the results of previous instructions in various ways. Every instruction in the code array has a number, starting with zero for the first instruction, that when used as an operand refers to its result. The combining opcodes are:
| Opcode | Operands | Operation |
|---|---|---|
| 0 | count, ... | add |
| 1 | count, ... | multiply |
| 2 | count, ... | maximum |
| 3 | count, ... | minimum |
| 4 | subtrahend, minuend | subtract |
| 5 | dividend, divisor | divide |
| 6 | negand | negate |
| 7 | idempotentate | identity |
Add, multiply, maximum and minimum all take variable numbers of arguments. The first argument is the number of operands, and the rest are indices of results computed by previous instructions. The identity operator does nothing useful, and is only included for the convenience of programs that automatically generate RenderMan input.
Let's look at an example. Here's the RIB input for the hand on the right in this picture.
Blobby 22 [ # code array 1001 0 # 0 1001 16 # 1 1001 32 # 2 1001 48 # 3 1001 64 # 4 1001 80 # 5 1001 96 # 6 1001 112 # 7 1001 128 # 8 1001 144 # 9 1001 160 # 10 1001 176 # 11 1001 192 # 12 1001 208 # 13 1001 224 # 14 1001 240 # 15 1001 256 # 16 1001 272 # 17 1001 288 # 18 1001 304 # 19 1001 320 # 20 1001 336 # 21 0 7 1 2 3 4 5 8 9 # 22 left finger sum 0 9 1 2 8 9 10 11 12 15 16 # 23 middle finger sum 0 7 8 9 15 16 17 18 19 # 24 right finger sum 0 6 13 14 15 16 20 21 # 25 thumb sum 0 11 0 1 2 6 7 8 9 13 14 15 16 # 26 palm sum 2 5 22 23 24 25 26 # 27 max of sums ] [ # float arguments 1. 0 0 0 0 1. 0 0 0 0 1. 0 -1.50 -1.20 0 1 # 0 1. 0 0 0 0 1. 0 0 0 0 1. 0 -1.50 -0.60 0 1 # 1 1. 0 0 0 0 1. 0 0 0 0 1. 0 -1.50 0.00 0 1 # 2 .8 0 0 0 0 1.2 0 0 0 0 .8 0 -1.50 0.60 0 1 # 3 .8 0 0 0 0 1.6 0 0 0 0 .8 0 -1.50 1.60 0 1 # 4 .8 0 0 0 0 1.4 0 0 0 0 .8 0 -1.50 2.60 0 1 # 5 1. 0 0 0 0 1. 0 0 0 0 1. 0 -1.05 -1.80 0 1 # 6 1. 0 0 0 0 1. 0 0 0 0 1. 0 -0.60 -1.20 0 1 # 7 1. 0 0 0 0 1. 0 0 0 0 1. 0 -0.60 -0.60 0 1 # 8 1. 0 0 0 0 1. 0 0 0 0 1. 0 -0.60 0.00 0 1 # 9 .8 0 0 0 0 1.2 0 0 0 0 .8 0 -0.60 0.60 0 1 # 10 .8 0 0 0 0 1.6 0 0 0 0 .8 0 -0.60 1.70 0 1 # 11 .7 0 0 0 0 1.6 0 0 0 0 .8 0 -0.60 2.70 0 1 # 12 1. 0 0 0 0 1. 0 0 0 0 1. 0 -0.15 -1.80 0 1 # 13 1. 0 0 0 0 1. 0 0 0 0 1. 0 0.30 -1.20 0 1 # 14 1. 0 0 0 0 1. 0 0 0 0 1. 0 0.30 -0.60 0 1 # 15 1. 0 0 0 0 1. 0 0 0 0 1. 0 0.30 0.00 0 1 # 16 .8 0 0 0 0 1.2 0 0 0 0 .8 0 0.30 0.60 0 1 # 17 .8 0 0 0 0 1.6 0 0 0 0 .8 0 0.30 1.60 0 1 # 18 .8 0 0 0 0 1.4 0 0 0 0 .8 0 0.30 2.60 0 1 # 19 .8 0 0 0 0 .8 0 0 0 0 .8 0 0.90 -1.05 0 1 # 20 1.4 0 0 0 0 .8 0 0 0 0 .8 0 1.80 -0.85 0 1 # 21 ] [ "" ] # string argumentsThe code array first specifies the 21 ellipsoid blobs that make up the hand, then the five sums that blend its various parts, then the max that combines the parts without inter-part blending. The float array contains the transformation matrices mapping the unit sphere onto each of the 21 ellipsoids. code max float
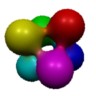
Parameter Values
The parameter list is a list of name-value pairs that are passed as arguments to shaders. Parameters can be uniform, with the same value at every point on the object, or varying, having different values at different points. The parameter list specifies a single value for uniform parameters, and one value for each primitive field (the instructions with opcodes >=1000) for varying parameters. Values from the primitive fields are combined appropriately as the combining operations are executed, so the values corresponding to combining operations need not (cannot!) be specified explicitly. For example, the picture at the very top of this document was drawn from this RIB:Blobby 6 [ 1001 0 # 0 1001 16 # 1 1001 32 # 2 1001 48 # 3 1001 64 # 4 1001 80 # 5 0 6 0 1 2 3 4 5 # 6 ] [ 1 0 0 0 0 1 0 0 0 0 1 0 0.89 0 0 1 # 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0.89 0 1 # 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0.89 1 # 2 1 0 0 0 0 1 0 0 0 0 1 0 -0.89 0 0 1 # 3 1 0 0 0 0 1 0 0 0 0 1 0 0 -0.89 0 1 # 4 1 0 0 0 0 1 0 0 0 0 1 0 0 0 -0.89 1 # 5 ] [ "" ] "vertex color Cs" [ 1 0 0 # 0 0 1 0 # 1 0 0 1 # 2 0 1 1 # 3 1 0 1 # 4 1 1 0 # 5 ]The code array specifies the sum of six blobs, positioned at the vertices of an octahedron. The surface color Cs is specified for each blob, but not for the sum. In the picture, the color blends appropriately as the blobs blend together. code Cs
Vertex values that are constant within each primitive blob are
fine for many purposes, but we also need to be able to specify
values that change from point to point within primitive blobs.
For example, we would like to be able to specify reference
coordinate systems for solid textures that will stick to surfaces
as their primitive blobs move. To that end, prman has a
new vertex value type mpoint. The value given in the
RIB stream for an mpoint value is a 4x4 matrix
that maps points from the primitive blob to the reference
coordinate system.
The values used at each surface point are obtained by transforming
points back from
object space to the primitive blob's coordinates (using the
inverse of the blob matrix), and thence (using the mpoint matrix)
into the reference space. Thus, as far
as the shader is concerned, the type of an mpoint value
is point, even though a matrix is specified in the
RIB stream.
Clear? I thought not. Here's the RIB input for the top surface in the image above:
Blobby 3 [ 1001 0 1001 16 1001 32 0 3 0 1 2 ] [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 2 0 0 1 ] [ "" ] "vertex mpoint Pref" [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 2 0 0 1 ] "color Cs" [.1 .9 .2] # these are the "color Ct" [.9 .2 .1] # colors of the checksThere are three blobs in a line. The transformations given for Pref are the same as those used to specify the object, so Pref will be the same as the blobby's object space coordinates. As you might expect, the solid-texture checkerboard mapped onto the surface is undistorted.
Now let's look at the RIB for the surface on the bottom of the same picture:
Blobby 3 [ 1001 0 1001 16 1001 32 0 3 0 1 2 ] [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 1 .3 0 1 1 0 0 0 0 1 0 0 0 0 1 0 2 0 0 1 ] [ "" ] "vertex mpoint Pref" [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 2 0 0 1 ] "color Cs" [.1 .9 .2] "color Ct" [.9 .2 .1]The only difference here is that we've translated the middle blob by .3 in y. In the image, the part of the solid texture that maps onto the middle blob has moved up with it, with some compensating distortion in the blends so that the texture on the other two blobs can stick as well. y
Caveat Emptor
The RiBlobby implementation stresses prman in ways that no previous gprim did. As a result, there are a few things to watch out for:- Always use
ShadingInterpolation "smooth"
Otherwise the shading on RiBlobby surfaces may have gritty artifacts. - The calculatenormal shadeop often produces poor results. This can cause trouble for displacement and bump-map shaders.
- If you use
Projection "orthographic"
you may get bad results. This is a theoretical problem only. RiBlobby's dicing code really only works correctly for perspective projections. In every test case we've run it's done just fine in the orthographic case, but dicing-rate problems could possibly come up. - Non-smooth surfaces can look nasty at their creases. In fact, this is a general problem with prman's strategy of dicing into micropolygons, but it doesn't often come up with other gprims.